Analysis of HIV Drug Resistance
STAT 2131 Course Final Project at Pitt
The scientific goal is to determine which mutations of the Human Immunodeficiency Virus Type 1 (HIV-1) are associated with drug resistance. The data set, publicly available from the Stanford HIV Drug Resistance Database Stanford HIV Drug Resistance Database, was originally analyzed in (Rhee et al. 2006).
Preparing the data
The data set consists of measurements for three classes of drugs: protease inhibitors (PIs), nucleoside reverse transcriptase (RT) inhibitors (NRTIs), and nonnucleoside RT inhibitors (NNRTIs). Protease and reverse transcriptase are two enzymes in HIV-1 that are crucial to the function of the virus. This data set seeks associations between mutations in the HIV-1 protease and drug resistance to different PI type drugs, and between mutations in the HIV-1 reverse transcriptase and drug resistance to different NRTI and NNRTI type drugs (The raw data are saved as gene_df).
In order to evaluate our results, we compare with the treatment-selected mutation panels created by (Rhee et al. 2005), which can be viewed as the ground true. These panels give lists of HIV-1 mutations appearing more frequently in patients who have previously been treated with PI, NRTI, or NNRTI type drugs, than in patients with no previous exposure to that drug type. Increased frequency of a mutation among patients treated with a certain drug type implies that the mutation confers resistance to that drug type (The raw data are saved as tsm_df).
To simplify the analysis, in this project we will confine our attention to the PI drugs.
drug_class = 'PI' # Possible drug types are 'PI', 'NRTI', and 'NNRTI'
Fetching and cleaning the data
First, we download the data and read it into data frames.
base_url = 'http://hivdb.stanford.edu/_wrapper/pages/published_analysis/genophenoPNAS2006'
gene_url = paste(base_url, 'DATA', paste0(drug_class, '_DATA.txt'), sep='/')
tsm_url = paste(base_url, 'MUTATIONLISTS', 'NP_TSM', drug_class, sep='/')
gene_df = read.delim(gene_url, na.string = c('NA', ''), stringsAsFactors = FALSE)
tsm_df = read.delim(tsm_url, header = FALSE, stringsAsFactors = FALSE)
names(tsm_df) = c('Position', 'Mutations')
A small sample of the data is shown below.
head(gene_df, n=6)
| APV | ATV | IDV | LPV | NFV | RTV | SQV | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.3 | NA | 32.7 | NA | 23.4 | 51.6 | 37.8 | - | - | - | - | - | - | - | - | - | I |
| 76.0 | NA | 131.0 | 200.0 | 50.0 | 200.0 | 156.0 | - | - | - | - | - | - | - | - | - | F |
| 2.8 | NA | 12.0 | NA | 100.0 | 41.0 | 145.6 | - | - | - | - | - | - | - | - | - | - |
| 6.5 | 9.2 | 2.1 | 5.3 | 5.0 | 36.0 | 13.0 | - | - | - | - | - | - | - | - | - | I |
| 8.3 | NA | 100.0 | NA | 161.1 | 170.2 | 100.0 | - | - | - | - | - | - | - | - | - | I |
| 82.0 | 75.0 | 400.0 | 400.0 | 91.0 | 400.0 | 400.0 | - | - | - | - | - | - | - | - | - | I |
head(tsm_df, n=6)
| Position | Mutations |
|---|---|
| 10 | F R |
| 11 | I |
| 20 | I T V |
| 23 | I |
| 24 | I |
| 30 | N |
In tsm_df, the variable Position denotes the position of the mutations that are associated with drug-resistance, while Mutations indicating the mutation type.
The gene data table has some rows with error flags or nonstandard mutation codes. For simplicity, we remove all such rows.
# Returns rows for which every column matches the given regular expression.
grepl_rows <- function(pattern, df) {
cell_matches = apply(df, c(1,2), function(x) grepl(pattern, x))
apply(cell_matches, 1, all)
}
pos_start = which(names(gene_df) == 'P1')
pos_cols = seq.int(pos_start, ncol(gene_df))
valid_rows = grepl_rows('^(\\.|-|[A-Zid]+)$', gene_df[,pos_cols])
gene_df = gene_df[valid_rows,]
Preparing the regression matrix
We now construct the design matrix \(X\) and matrix of response vectors \(Y\). The features (columns of \(X\)) are given by mutation/position pairs. Define
\[X_{i,j} = 1 \text{ if the } i \text{th patient has the } j \text{th mutation/position pair and 0 otherwise}\] \[Y_{i,k} = \text{resistance of patient } i \text{ to drug } k.\]For example, in the sample for PI type drugs, three different mutations (A, C, and D) are observed at position 63 in the protease, and so three columns of \(X\) (named P63.A, P63.C, and P63.D) indicate the presence or absence of each mutation at this position.
# Flatten a matrix to a vector with names from concatenating row/column names.
flatten_matrix <- function(M, sep='.') {
x <- c(M)
names(x) <- c(outer(rownames(M), colnames(M),
function(...) paste(..., sep=sep)))
x
}
# Construct preliminary design matrix.
muts = c(LETTERS, 'i', 'd')
X = outer(muts, as.matrix(gene_df[,pos_cols]), Vectorize(grepl))
X = aperm(X, c(2,3,1))
dimnames(X)[[3]] <- muts
X = t(apply(X, 1, flatten_matrix))
mode(X) <- 'numeric'
# Remove any mutation/position pairs that never appear in the data.
X = X[,colSums(X) != 0]
# Extract response matrix.
Y = gene_df[,4:(pos_start-1)]
An excerpt of the design matrix is shown below. By construction, every column contains at least one 1, but the matrix is still quite sparse with the relative frequency of 1’s being about 0.025.
library(DT)
datatable(data.frame(X)[1:10, ], options = list(scrollX=T, pageLength = 10))
| P4.A | P12.A | P13.A | P16.A | P20.A | P22.A | P28.A | P37.A | P51.A | P54.A |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
The response matrix looks like:
head(Y, n=6)
There are 7 PI-type drugs: APV, ATV, IDV, LPV, NFV, RTV, and SQV.
| APV | ATV | IDV | LPV | NFV | RTV | SQV |
|---|---|---|---|---|---|---|
| 2.3 | NA | 32.7 | NA | 23.4 | 51.6 | 37.8 |
| 76.0 | NA | 131.0 | 200.0 | 50.0 | 200.0 | 156.0 |
| 2.8 | NA | 12.0 | NA | 100.0 | 41.0 | 145.6 |
| 6.5 | 9.2 | 2.1 | 5.3 | 5.0 | 36.0 | 13.0 |
| 8.3 | NA | 100.0 | NA | 161.1 | 170.2 | 100.0 |
| 82.0 | 75.0 | 400.0 | 400.0 | 91.0 | 400.0 | 400.0 |
Selecting drug-resistance-associated mutations
In this step, I impose a linear regression model, and use the method I learned in lecture to select mutations that may associated with drug-resistance. For 7 PI-type drugs, I run a separate analysis for each drug.
Notice that there are some missing values.
Before selecting associated mutations, we need to perform some final pre-processing steps. We remove rows with missing values (which vary from drug to drug) and we then further reduce the design matrix by removing predictor columns for mutations that do not appear at least three times in the sample. Finally, for identifiability, we remove any columns that are duplicates (i.e. two mutations that appear only in tandem, and therefore we cannot distinguish between their effects on the response).
A quick inspection of the response vector shows that it is highly non-Gaussian.
hist(Y[,1], breaks='FD')
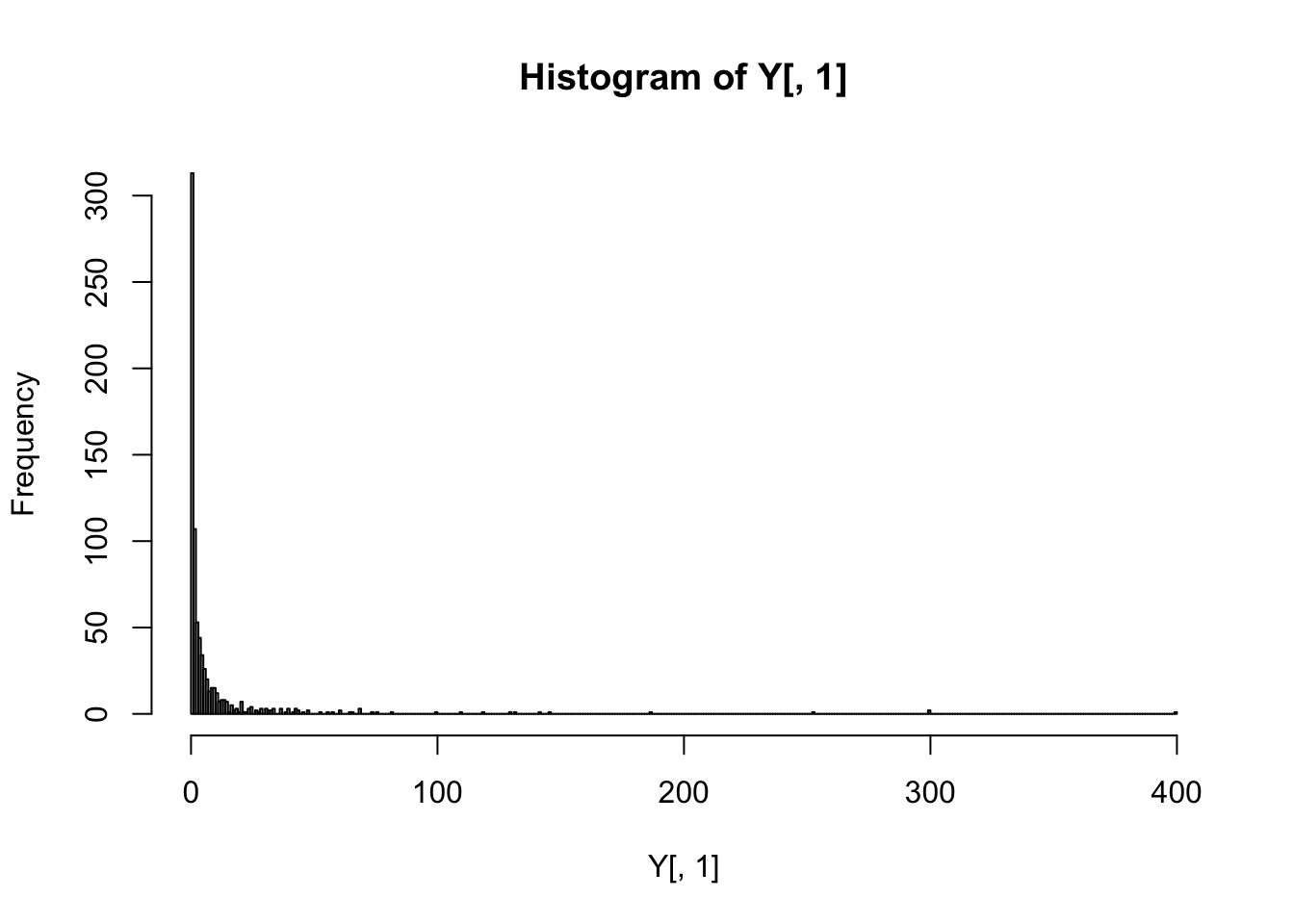
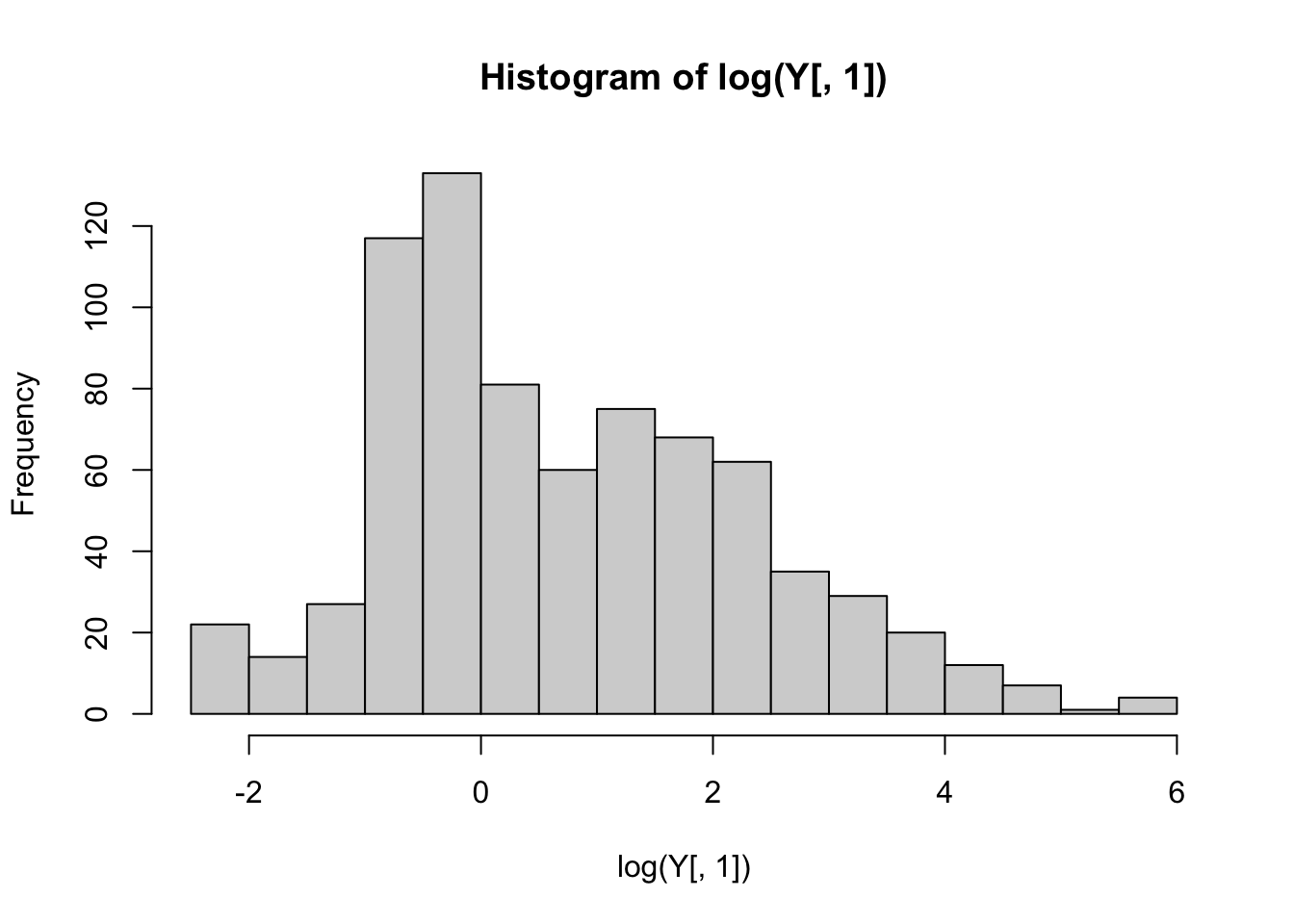
A log-transform seems to help considerably, so we will use the log-transformed drug resistancement measurements below.
hist(log(Y[,1]), breaks='FD')
selection <- function (X, y, alpha) {
# Remove patients with missing measurements.
missing = is.na(y)
y = y[!missing]
X = X[!missing,]
# Remove predictors that appear less than 3 times.
X = X[,colSums(X) >= 3]
# Remove duplicate predictors.
X = X[,colSums(abs(cor(X)-1) < 1e-4) == 1]
# Based on an appropriate linear regression model
# Select the mutations that may associated with drug-resistance
y_log <- log(y)
data <- as.data.frame(cbind(y_log, X))
model <- lm(y_log ~ . , data = data)
# Extract p-values for each predictor
p_values <- summary(model)$coef[, "Pr(>|t|)"]
# Adjust p-values for controlling the FWER using Bonferroni correction
adjusted_p_values <- p.adjust(p_values, method = "bonferroni")
# Select mutations with adjusted p-values below the alpha threshold
selected_mutations <- names(which(adjusted_p_values < alpha))
selected_mutations <- selected_mutations[-1]
return(selected_mutations)
}
alpha = 0.05 # the nominal FWER
# Create a vector with the names of PI-type drugs
pi_drug_names <- c("APV", "ATV", "IDV", "LPV", "NFV", "RTV", "SQV")
results = lapply(Y, function(y) selection(X, y, alpha))
for(i in 1:7){
cat(pi_drug_names[i], ":", results[[i]], "\n\n")}
The output is
APV : P84.A P84.C P10.F P33.F P82.F P10.I P46.I P50.L P54.L P54.M P90.M P88.S P10.V P47.V P50.V P76.V P84.V
ATV : P90.M P73.S P88.S P20.T P48.V P54.V P76.V P84.V
IDV : P54.A P82.A P84.A P84.C P10.F P82.F P10.I P20.I P24.I P46.I P50.L P48.M P90.M P54.S P73.S P88.S P54.T P73.T P82.T P48.V P54.V P71.V P76.V P84.V
LPV : P82.A P84.A P10.F P33.F P82.F P10.I P46.I P50.L P48.M P82.S P54.T P47.V P48.V P50.V P54.V P76.V P84.V
NFV : P84.C P10.F P82.F P10.I P20.I P24.I P46.I P50.L P54.M P90.M P30.N P63.P P73.S P74.S P88.S P20.T P54.T P73.T P48.V P54.V P71.V P84.V
RTV : P82.A P84.A P84.C P33.F P82.F P24.I P46.I P50.L P90.M P63.P P82.S P20.T P54.T P82.T P48.V P50.V P54.V P84.V
SQV : P82.A P84.A P84.C P88.D P10.F P82.F P10.I P20.I P24.I P10.L P50.L P53.L P48.M P90.M P54.S P73.S P88.S P54.T P48.V P54.V P71.V P76.V P84.V
Evaluating the results
In this case, we are fortunate enough to have a “ground truth” obtained by another experiment (data saved as tsm_df). Using this, we can evaluate the selected results. Note that we only need to compare the position of the mutations, not the mutation type. This is because it is known that multiple mutations at the same protease or RT position can often be associated with related drug-resistance outcomes.
# Evaluate the result by comparing it to the ground true
# Create a vector with the names of PI-type drugs
pi_drug_names <- c("APV", "ATV", "IDV", "LPV", "NFV", "RTV", "SQV")
# Function to extract positions from mutation strings
get_positions <- function(mutations) {
unique(sapply(strsplit(mutations, "\\."), "[", 1))
}
# Prepend "P" to tsm_df$Position for comparison
tsm_df$Position <- paste("P", tsm_df$Position, sep = "")
# Evaluate the result for each PI-type drug
for (i in seq_along(Y)) {
selected_mutations <- results[[i]]
if (!is.null(selected_mutations)) {
# Get the positions from selected mutations
selected_positions <- get_positions(selected_mutations)
# Get the positions from the ground truth for the corresponding drug
true_positions <- tsm_df$Position[tsm_df$Position %in% selected_positions]
# Calculate the overlap between selected and true positions
overlap <- length(intersect(selected_positions, true_positions))
# Output the evaluation metrics
cat("Drug:", pi_drug_names[i], "\n")
cat("Selected Positions:", selected_positions, "\n")
cat("True Positions:", true_positions, "\n")
cat("Overlap:", overlap, "\n")
cat("Precision:", overlap / length(selected_positions), "\n")
cat("Recall:", overlap / length(true_positions), "\n")
cat("------------------------------\n")
}
}
The output is
Drug: APV
Selected Positions: P84 P10 P33 P82 P46 P50 P54 P90 P88 P47 P76
True Positions: P10 P33 P46 P47 P50 P54 P76 P82 P84 P88 P90
Overlap: 11
Precision: 1
Recall: 1
------------------------------
Drug: ATV
Selected Positions: P90 P73 P88 P20 P48 P54 P76 P84
True Positions: P20 P48 P54 P73 P76 P84 P88 P90
Overlap: 8
Precision: 1
Recall: 1
------------------------------
Drug: IDV
Selected Positions: P54 P82 P84 P10 P20 P24 P46 P50 P48 P90 P73 P88 P71 P76
True Positions: P10 P20 P24 P46 P48 P50 P54 P71 P73 P76 P82 P84 P88 P90
Overlap: 14
Precision: 1
Recall: 1
------------------------------
Drug: LPV
Selected Positions: P82 P84 P10 P33 P46 P50 P48 P54 P47 P76
True Positions: P10 P33 P46 P47 P48 P50 P54 P76 P82 P84
Overlap: 10
Precision: 1
Recall: 1
------------------------------
Drug: NFV
Selected Positions: P84 P10 P82 P20 P24 P46 P50 P54 P90 P30 P63 P73 P74 P88 P48 P71
True Positions: P10 P20 P24 P30 P46 P48 P50 P54 P71 P73 P74 P82 P84 P88 P90
Overlap: 15
Precision: 0.9375
Recall: 1
------------------------------
Drug: RTV
Selected Positions: P82 P84 P33 P24 P46 P50 P90 P63 P20 P54 P48
True Positions: P20 P24 P33 P46 P48 P50 P54 P82 P84 P90
Overlap: 10
Precision: 0.9090909
Recall: 1
------------------------------
Drug: SQV
Selected Positions: P82 P84 P88 P10 P20 P24 P50 P53 P48 P90 P54 P73 P71 P76
True Positions: P10 P20 P24 P48 P50 P53 P54 P71 P73 P76 P82 P84 P88 P90
Overlap: 14
Precision: 1
Recall: 1
------------------------------
Building a linear model for prediction
In this part, we consider building a linear model for predicting drug resistance to APV. We extract all mutations at those positions provided by the file tsm_df.
get_name<-function(x){return(outer(x["Position"], unlist(strsplit(x["Mutations"], split =" ")), function(...) paste(..., sep=".")))}
mutation_name <- unlist(apply(tsm_df, 1, get_name))
# mutation_name <- paste("P", unlist(apply(tsm_df, 1, get_name)), sep="")
col_index <- which(colnames(X) %in% mutation_name)
candidate_X <- X[, col_index]
We need to build a model by using candidate explanatory variables provided by candidate_X above. Build a model for prediction with an appropriate model selection criterion, which can be either AIC, BIC, or leave-one-out cross-validation error.
library(leaps)
# Model selection and prediction
# Set the seed for reproducibility
set.seed(10086)
# Remove missing value
missing <- is.na(Y[,"APV"])
Y <- Y[!missing,]
candidate_X <- candidate_X[!missing,]
# Remove predictors that appear less than 3 times.
candidate_X = candidate_X[,colSums(candidate_X) >= 3]
# Remove duplicate predictors.
candidate_X = candidate_X[,colSums(abs(cor(candidate_X)-1) < 1e-4) == 1]
# Split the data into training and testing sets
n <- nrow(candidate_X)
train_indices <- sample(1:n, round(0.7 * n)) # 70% for training
test_indices <- setdiff(1:n, train_indices)
# Create training and testing datasets
train_X <- as.data.frame(candidate_X[train_indices, ])
test_X <- candidate_X[test_indices, ]
train_y <- Y[train_indices, "APV"]
test_y <- Y[test_indices, "APV"]
log_train_y <- log(train_y)
log_test_y <- log(test_y)
# Build a linear regression model using forward stepwise selection
model <- regsubsets(log_train_y ~ ., data = cbind(log_train_y,train_X), method = "forward")
# Get the best model based on the BIC criterion
best_model_index <- which.min(summary(model)$bic)
selected_predictors <- names(coef(model, id = best_model_index))
selected_predictors <- selected_predictors[-1]
# Build the final linear regression model using the selected predictors
final_model <- lm(log_train_y ~ ., data = as.data.frame(train_X[, c(selected_predictors)]))
final_model
# Predict drug resistance on the test set using the final model
predictions <- predict(final_model, newdata = as.data.frame(test_X[, c(selected_predictors)]))
# Evaluate the model
MSPR <- mean((predictions - log_test_y)^2)
MSE <- mean(summary(final_model)$residuals^2)
# Output evaluation metrics
cat("Mean Square Prediction Error (MSPR):", MSPR, "\n")
cat("Mean Square Error (MSE):", MSE, "\n")
The output is
Call:
lm(formula = log_train_y ~ ., data = as.data.frame(train_X[,
c(selected_predictors)]))
Coefficients:
(Intercept) P82.A P84.A P33.F P46.I
-0.2474 0.9822 3.2157 1.3097 0.8561
P90.M P88.S P50.V P84.V
0.7603 -1.8503 2.2609 1.0575
Mean Square Prediction Error (MSPR): 0.8408786
Mean Square Error (MSE): 0.7267954
MSPR is close to MSE, which indicates that the model is valid.
References
Rhee, Soo-Yon, W Jeffrey Fessel, Andrew R Zolopa, Leo Hurley, Tommy Liu, Jonathan Taylor, Dong Phuong Nguyen, et al. 2005. “HIV-1 Protease and Reverse-Transcriptase Mutations: correlations with Antiretroviral Therapy in Subtype B Isolates and Implications for Drug-Resistance Surveillance.” Journal of Infectious Diseases 192 (3). Oxford University Press: 456–65.
Rhee, Soo-Yon, Jonathan Taylor, Gauhar Wadhera, Asa Ben-Hur, Douglas L Brutlag, and Robert W Shafer. 2006. “Genotypic Predictors of Human Immunodeficiency Virus Type 1 Drug Resistance.” Proceedings of the National Academy of Sciences 103 (46). National Academy of Sciences: 17355–60.